Kessler szindróma

A forgó kör kerületi sebessége nagyban függ a középponttól való távolságtól.

(Na, sikerült az első mondattal az olvasók nagyobbik részét elriasztanom. Azért birkózz tovább légyszíves, nem lesz ilyen érthetetlen!)

Ennek rengeteg példázatát szokták emlegetni a súlylökő láncon pörgetett nehezékétől a jégtáncos felgyorsuló pörgéséig.

Nekem a néphadseregnek csúfolt, léleknyomorító intézmény egyik kínzóeszköze, a menetelés jut róla eszembe. Órákig menetelni, körbe-körbe a betonon, egy 10-12 fő széles menetoszlopban semmi lélekemelő nincs.

Ilyenkor nem a hazaszeretet fogalmán rágódik az ember, hanem a fizika fentebb említett tétele töri fel a talpát. A széles, egyszerre lépő sor a betonpálya végén visszafordul. A belső ember ilyenkor helybenjár, míg a sor szélén lévőknek bakugrásokat kell tenni, hogy azonos lépésszám mellett ne maradjon le, és a sor egyenesen forduljon. A fizikától távolálló, sötét analfabéták is hamar belátták, hogy a sor külső szélére kerülni a szivatás kategória alá sorolható. Minél szélesebb a sor, annál nagyobb lesz fordulásnál a kerületi sebesség, így tarthatatlan lesz a szélén a sor egyenessége.

A fenti szabály jól nyomonkövethető a Föld forgásánál is.

A bolygó egy nap, azaz 24 óra alatt fordul meg a tengelye körül. A menetelők ezen csak sajnálkozva mosolyogtak, hiszen mi egy nap alatt legalább hússzor megfordultunk.

Azonban a Föld körül menetelő sor jóval szélesebb, középpontjától a felszínen álló ember 6370km távolságra van. Neki már 40.000km-t — ilyen hosszú az egyenlítő — kell megtenni naponta, hogy ne maradjon le! Vagyis 40.000km/24óra 1670km/órával kell szaladni. Kevesen gondolnak ebbe bele, hogy ilyen sebességgel száguldva pörgünk itt a földfelszínen. Ilyen sebességet már csak a szuperszónikus repülőgépek és rakéták tudnak elérni. Itt nekem is le kell írni azt a példát, hogy a kelet felé tartó szuperszónikus gépen ülő ember, aki a földfelszínhez képest 1670km/h sebességgel száguld, folyamatosan egy helyben fogja látni a napot. Hiszen valójában csak a Föld forgását kompenzálja ezzel a sebességgel, és a Napból nézve egy helyben áll.

Most képzelj el egy centrifugát! Milyen erővel présel oda a falhol a gyors forgás!

Ezek a szabályok a Földtől távolabb lévő testekre, a bolygó körül keringő testekre és műholdakra is igazak.

Ha ilyen sebességgel kering egy test, ott már olyan erővel akar “kirepülni a centrifugából”, ami a Föld gravitációját is képes ellensúlyozni. Ha a sebesség miatt a centrifuga ereje pont akkora, mint a gravitáció, akkor a test lebegni fog.

Majd’ 100 évvel ezelőtt, a “2001 Űrodisszeia” írója, Sir Arthur C. Clarke elkezdett számolni. Van-e olyan távolság a Földtől, ahol akkora sebességgel száguldhat egy műhold, hogy a centrifuga ereje megegyezzen a gravitációval és pont egy nap alatt tegyen meg egy kört?!

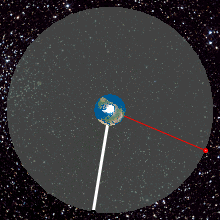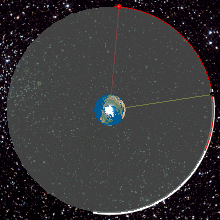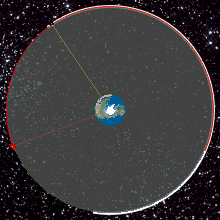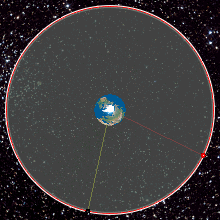
És igen, megtalálta! A geostacionárius pályán keringő műhold, mivel együtt mozog a Földdel, így a földfelszínről nézve mindig egy helyben áll a levegőben!

A pálya magassága 35 786 km az átlagos tengerszint fölött. Szép távolság. És milyen gyorsan kell ott “futni” a virtuális menetoszlop szélén? Itt bizony már 11000km/h sebességgel kell haladni ahhoz, hogy ne kerüljön fogdába a lusta menetelő.

Rengeteg műhold van már fönn a Föld körül. Mivel a geostacionárius pálya túl messze van, ezért sokkal több olyan műhold van, ami száguldozik körülöttünk, és nem mindig egy helyben látszik. Ha közelebb van, akkor nagyobb sebességgel kell “pörgetni”, hogy le ne essen, azaz a kerületi sebesség növelésével kompenzálni a gravitációt. Ezek a műholdak 42.000km/h sebességgel száguldanak! Ez tízszer nagyobb sebesség, mint egy puskagolyóé!

Na és akkor már mindent tudsz ahhoz, hogy a Kessler-szindrómát szóba hozzam.

Amikor egy űrállomásról levált festékdarab a puskagolyó tízszeres sebességével becsapódik a vele szembehaladó műholdba, akkor azt képes darabokra szaggatni. Most képzeld el mit csinálhat akkor a kőkeményre fagyott kakizacsi, amit talán még Gagarin hajított ki! Nem kitérve az ötven éve mínusz egy nap elfogyasztott vacsora mennyiségére…

Kessler 1978(!)-ban hívta fel a figyelmet az űrszemét problémájára.

Ha láttad már billiárd játék kezdetét, akkor előtted van a kép, ahogy a háromszög alakzatba összerendezett golyók miként robbannak szanaszét a becsapodó golyótól. Most képzeld el, ha hússzor nagyobb erővel csapódik be az a fehér golyó!

Az űrben kb 6.500.000kg űrszemét kering már, aminek nagy részéről nincs meg a pályaadat! Egy csavar becsapódása olyan láncreakciót válthat ki, ami szinte pillanatok alatt minden műholdat további darabokra szakít, így egyik napról a másikra minden műholdas rendszer összeomlik.

Az internet, a GPS, a banki rendszerek, minden tranzakció azonnal megáll.

Ma már olyan szinten épül minden az informatikai hálózatra, hogy annak leállása a legbrutálisabb forgatókönyveket vizionálja.

Amikor majd ülsz a fűtetlen, sötét, pöcegödör szagú szobában (a szennyvíz-elvezetés is komoly infrastruktúrúra épül), lehet hogy pont Gagarin túlfűszerezett borscslevesének átka sújtott ránk…